Θερμοκρασία. Ανάλυση ενός από τα θεμελειώδη φυσικά μεγέθη.

Η θερμοκρασια ειναι μια απο τις σημαντικοτερες μεταβλητες και φυσικα μεγεθη στην μετεωρολογια αλλά και στην καθημερινοτητα του ανθρωπου.

Η αναγκη ποσοτικοποιησης της αισθησης μας για κρυο ή ζεστο προερχεται απο την τελειως υποκειμενικη αισθηση που εχει καθε ανθρωπος για το τι ειναι κρυο ή ζεστο και βεβαια για την ορθη μελετη των φυσικων φαινομενων.
Μιας και η εννοια του θερμο/ψυχρο ειναι τελειως σχετικη, αφου πχ εαν βαλουμε το χερι μας σε ενα δοχειο με νερο θερμοκρασιας 35 °C θα μας φανει σχετικα ζεστο, ενω αμα βαλουμε πρωτα το χερι μας σε δοχειο με νερο θερμοκρασιας 1 °C και μετα αμεσως το βαλουμε στο προηγουμενο δοχειο των 30 °C θα μας φανει καυτο, οποτε χρειαζομαστε μια μεταβλητη που περιγραφει αντικειμενικα το πόσο κρυο ή ζεστο ειναι ενα σωμα και δινοντας του και μια τιμη για την ποσοτητα κρυου ή ζεστου.

Τι ειναι ομως η «θερμοκρασια»?
Οπως ξερουμε τα σωματα αποτελουνται απο μορια(ή ιοντα ή ατομα) που βρισκονται σε μια διαρκη χαοτικη κινηση. Σε ενα αεριο τα μορια του εκτελουν συνεχως πολυ ατακτες κινησεις μεσα στον χωρο που βρισκεται το αεριο προς οποιαδηποτε κατευθυνση θελουνε, ενω σε ενα υγρο πχ σε ενα μπουκαλι η κινηση ειναι πιο περιορισμενη και παλι ομως με ατακτη κινηση των μοριων προς οποιαδηποτε κατευθυνση, ενω ακομα πιο περιορισμενη και διαφορετικου ειδους ειναι η κινηση σε ενα στερεο, πχ ενα μολυβι, οπου τα μορια του εκτελουν πολυ μικροτερης εκτασης κινησεις περιορισμενα μεσα στο κρυσταλλικο πλεγμα τους γυρω απο την μεση θεση ισορροπιας τους.
Και ο αριθμος των μοριων σε καθε σωμα ειναι τεραστιος, πχ σε μολις 32 γραμμαρια αεριου οξυγονου περιεχονται 600 000 000 000 000 000 000 000 (600 εξακις εκατομμυρια) μορια!
Τα μορια ενος σωματος βεβαια δεν εκτελουν μόνο τις εσωτερικες χαοτικες κινησεις που αναφερθηκαν, αλλά υποκεινται και στην εξωτερικη του σωματος κινηση οπως πχ η κινηση λογω της περιστροφης της γης γυρω απο τον εαυτο της, γυρω απο τον ηλιο, εως και την κινηση του γαλαξια ως προς τον χωρο. Ή ακομα κινησεις λογω πχ πτωσης του σωματος απο ενα υψος, κινηση των μοριων του νερου της θαλασσας λογω κυματισμου, κλπ.

Εμας μας ενδιαφερει ομως, διοτι ειναι αυτη η αιτια που δημιουργει τα θερμικα αποτελεσματα και την εννοια της θερμοκρασιας σε ενα σωμα, μόνο η 1η κινηση των μοριων, η εσωτερικη δηλαδη κινηση μεσα στο σωμα. Την εσωτερικη κινητικη ενεργεια δηλαδη των σωματων. Την οποια και καλουμε εσωτερικη ενεργεια του σωματος που ειναι η κινητικη ενεργεια λογω της κινησης των μοριων του εκτός της μεταφορικης κινητικης ενεργειας που εχουν τα μορια θεωρωντας τα ως ολον και εκτός της δυναμικης ενεργειας των μοριων του απο επιδρασεις εξωτερικων δυναμεων.
Η εσωτερικη ενεργεια ενος σωματος καλειται και θερμικη ενεργεια.

Ετσι λοιπον ενα πλαστικο παιχνιδι που κινειται μεσα σε ενα αυτοκινητο εχει ενεργεια λογω α)των κινησεων των μοριων του μεσα στο ιδιο το πλαστικο ως προς μια μεση θεση ισορροπιας ως προς την μεση θεση των μοριων του πλαστικου, β)της κινησης των μοριων του πλαστικου ως προς την γη(κινητικη ενεργεια) λογω μεταφορας του απο το αυτοκινητο, γ)της κινησης των μοριων του μολυβιου ως προς ενα σταθερο σημειο στον γαλαξια(κινητικη ενεργεια) λογω μεταφορας του απο την γη(και περιστροφικη κινηση και περιφορας της γυρω απο τον ηλιο), δ)της κινησης των μοριων του μολυβιου ως προς ενα σταθερο σημειο στον χωρο(κινητικη ενεργεια) λογω μεταφορας του απο τον γαλαξια μεσα στον χωρο καθως και διάφορες αλλες κινησεις.
Η εσωτερικη του ενεργεια ομως ειναι μόνο λογω του α).

Η θερμοκρασια λοιπον εκφραζει την ποσοτητα αυτης της εσωτερικης ενεργειας καθε σωματος.
Μεγαλη εσωτερικη ενεργεια σημαινει και μεγαλη θερμοκρασια. Μικρη εσωτερικη ενεργεια σημαινει και μικρη θερμοκρασια.
Ή ακριβεστερα, η εσωτερικη ενεργεια και η απολυτη θερμοκρασια ειναι μεγεθη ευθεως αναλογα.
(*το πρωθυστερο της απολυτης θερμοκρασιας θα εξηγηθει λιγο παρακατω)

Ενω καθε μεταβολη της εσωτερικης ενεργειας ενος σωματος αλλαζει και την θερμοκρασια του.
Οπου πχ αν τα μορια ενος υγρου σε ενα δοχειο, ως προς την εσωτερικη κινηση τους παντα μιλωντας, κινουνται με μια συγκεκριμενη μεση ταχυτητα, εχοντας μια θερμοκρασια, τοτε εαν τους δωθει ενεργεια ωστε να αυξησουν αυτην την μεση ταχυτητα που κινουνται, τοτε η θερμοκρασια θα αυξηθει.
Οποιαδηποτε τετοια ενεργεια δωθει ή αφαιρεθει απο ενα σωμα ωστε να αλλαξει την εσωτερικη ενεργεια του σωματος, καλειται και αυτη θερμικη ενεργεια, και η διαδικασια διακινησης της μεταξυ 2 σωματων ονομαζεται θερμοτητα.
Ετσι θερμοτητα ειναι ενας μηχανισμος διακινησης της θερμικης ενεργειας, οταν λεμε δηλαδη οτι σε ενα σωμα μεταφερθηκε θερμοτητα εννοουμε οτι μεταφερθηκε θερμικη ενεργεια με τον μηχανισμο της θερμοτητας.
Η παγκοσμια βιβλιογραφια ομως σε αυτο ειναι διφορουμενη και υπαρχει και η 2η «σχολη» που οριζει τις 2 εννοιες «θερμοτητας» και «θερμικης ενεργειας» ως ταυτοσημες.

Ετσι λοιπον η θερμοκρασια ενος σωματος, ειναι ενα μέτρο για το πόσο μεγαλη ειναι η εσωτερικη ενεργεια του σωματος, το πόσο γρηγορα δηλαδη κινουνται τα μορια μεσα του ως προς τις εσωτερικες τους κινησεις παντα.
Ενω την θερμοκρασια την μετραμε με τα θερμομετρα.

Να ορισουμε τωρα αυστηρως τι ειναι ακριβως η θερμοκρασια.
Για να γινει αυτο πρεπει να σκεφτουμε τι αντιπροσωπευει, και οπως ειπαμε ειναι ενα μέτρο για το πόσο μεγαλη ειναι η εσωτερικη ενεργεια του σωματος, που ειναι απλως η κινητικη ενεργεια των μοριων του σωματος μιλωντας παντα για τις τυχαιες εσωτερικες κινησεις τους.
Ετσι αν ολα τα μορια ενος σωματος εχουν καποιες ταχυτητες(μιλωντας παντα σε σχεση με τις εσωτερικες κινησεις μεσα στο σωμα) απο u-min εως u-max πχ, τοτε αν η μεση ταχυτητα τους ειναι u, τοτε η μεση κινητικη ενεργεια τους ειναι (1/2)·mu² οπου m η μεση μαζα των μοριων.
Αρα η εσωτερικη ενεργεια Ε ειναι ιση με Ε = (1/2)·mu²

Ετσι οριζουμε την απολυτη θερμοκρασια Τ ως μια ποσοτητα ευθεως αναλογη με την Ε, δηλαδη ισχυει Τ = κ·Ε
Αρα η απολυτη θερμοκρασια ενος σωματος ειναι ευθεως αναλογη με την μεση κινητικη ενεργεια των μοριων του σωματος, μιλωντας παντα για τις τυχαιες εσωτερικες κινησεις των μοριων μεσα στο σωμα.

Ετσι με βαση αυτον τον ορισμο 2 σωματα με διαφορετικες θερμοκρασιες εχουν και διαφορετικες μεσες κινητικες ενεργειες των μοριων τους.
Ενω αν φερουμε σε επαφη 2 σωματα με διαφορετικες θερμοκρασιες, τοτε η θερμικη ενεργεια θα ρεει γενικα απο το σωμα με την μεγαλυτερη θερμοκρασια(θερμοτερο σωμα) στο σωμα με την μικροτερη(ψυχροτερο). Το γενικα, εχει την σημασια οτι θα ρεει και απο το ψυχροτερο στο θερμοτερο αλλά η γενικη φορά που θα επικρατει ειναι απο το θερμοτερο προς το ψυχροτερο.

Ενω οταν 2 σωματα εχουν ιδια θερμοκρασια λεμε οτι βρισκονται σε θερμικη ισορροπια.

Πως ομως μπορουμε να μετρησουμε την απολυτη θερμοκρασια?
Επισης οπως γινεται φανερο ο όρος «θερμοκρασια» δεν ειναι καλως ορισμενος εως τωρα.
Για να επιλυθει αυτο πρεπει να δουμε τι εννοουμε συνηθως με τον όρο θερμοκρασια και σε τι αναφερεται αυτο.

Για την μετρηση λοιπον της θερμοκρασιας χρησιμοποιουμε καποιες ιδιοτητες των σωματων που εξαρτωνται απο την απολυτη θερμοκρασια του σωματος, οπως η γραμμικη διαστολη των στερεων, ο ογκος υγρων και αεριων, η ηλεκτρικη αντισταση αγωγων, η πιεση αεριων, κλπ, οι οποιες λεγονται θερμομετρικες ιδιοτητες. Βαση αυτων των ιδιοτητων λοιπον μπορουμε και μετραμε την θερμοκρασια, εκμεταλλευομενοι πχ οτι ο υδραργυρος οταν αυξανετια η θερμοκρασια αυξανει σε ογκο, οπως και τα περισσοτερα στερεα και υγρα αλλά και αερια.
Ετσι επιλεγοντας μια θερμομετρικη ιδιοτητα, πχ τον ογκο υγρου(πχ υδραργυρου) που εξαρταται απο την απολυτη θερμοκρασια και παιρνοντας ενα οργανο που να μπορει να μετρηθει αυτος ο ογκος, οπως πχ ενα θερμομετρο υδραργυρου, βαθμολογουμε καποιο σημειο ως μια συγκεκριμενη θερμοκρασια συνηθως στο σημειο τηξεως του νερου και βαθμολογουμε ενα αλλο σημειο σε ενα αλλο σημειο(οπου ο ογκος του υδραργυρου εχει αλλαξει) συνηθως στο σημειο βρασμου του νερου και το χωριζουμε σε ισες αποστασεις ενδιαμεσα και το προεκτεινουμε κιολας.
Ετσι, οι θερμοκρασιες που μετραμε με αυτον τον τροπο λεγονται εμπειρικες και τις συμβολιζουμε συνηθως με Θ.

Μια θερμομετρικη ιδιοτητα Χ για να ειναι καταλληλη για την δημιουργια ενος αναλογικου θερμομετρου πρεπει για ισες μεταβολες της Χ να παιρνουμε και ισες μεταβολες της Θ.
Δηλαδη να ισχυει καποια σχεση της μορφης: ΔΧ = λ·ΔΘ με λ που δεν εξαρταται απο το Θ ή το Χ, δηλαδη Χ = Χο + λ·(Θ – Θο) οπου Θο και Χο η εμπειρικη θερμοκρασια και η θερμομετρικη ιδιοτητα αντιστοιχα, σε μια αρχικη κατασταση.

Ετσι παιρνοντας 2 καταστασεις τις τ(πχ σημειο τηξης και πιο συγκεκριμενα την θερμοκρασια που δειχνει το θερμομετρο σε επαφη με τηκομενο παγο) και β(σημειο βρασμου και πιο συγκεκριμενα την θερμοκρασια που δειχνει το θερμομετρο σε επαφη με ατμους νερου που βραζει) με Χβ > Χο (θεωρωντας για ευκολια Χτ = Χο) και τις αντιστοιχες θερμοκρασιες Θβ , Θο (Θβ > Θο).
Ετσι για τυχαια θερμοκρασια Θ με τιμη της θερμομετρικης ιδιοτητας Χ, ισχυει:
Χ = Χο + λ·(Θ – Θο)
ενω για τις Χβ και Θβ ισχυει:
Χβ = Χο + λ·(Θβ – Θο) απο οπου παιρνουμε λ = (Χβ-Χο)/(Θβ-Θο)
οποτε και γενικα θα ισχυει:
Χ = Χο + ((Χβ-Χο)/(Θβ-Θο))·(Θ – Θο) αρα και:
Χ = Χο· (1 + (1/Χο)·((Χβ-Χο)/(Θβ-Θο))·(Θ – Θο)) (1)
ή αλλιως θετοντας α = (1/Χο)·(Χβ-Χο)/(Θβ-Θο) θα εχουμε οτι:
Χ = Χο·(1 + α(Θ-Θο)) (2)

Ο α λεγεται θερμικος συντελεστης της ιδιοτητας Χ και εχει διαστασεις αντιστροφης θερμοκρασιας.
Ενα ενδιαφερον χαρακτηριστικο του α για παρα πολλες θερμομετρικες ιδιοτητες ειναι οτι εχει σχετικα σταθερη τιμη για παρα πολλα υλικα για καθε θερμομετρικη ιδιοτητα και για πολυ μεγαλα ευρη θερμοκρασιων.

Για την κατασκευη λοιπον της πλεον ευρεως χρησιμοποιουμενης κλιμακας Κελσιου, οπως αυτη χρησιμοποιουνταν απο το 1743 εως το 1954 διαλεξαμε Θο = 0 (κατασταση οπου υγρο νερο και παγος βρισκονται σε ισορροπια κατω απο πιεση 1 atm, να εχουμε θερμοκρασια νερου στο σημειο παγου δηλαδη) και Θβ = 100 (κατασταση θερμοκρασιας ατμων νερου που βραζει υπο πιεση 1 atm) οποτε συμφωνα με τον τυπο (1) θα ισχυει:
Θ = 100·(Χ-Χο)/(Χβ-Χο) οποτε και καθε μεταβολη της θερμοκρασιας δινει ευθεως αναλογη μεταβολη της ιδιοτητας Χ αφου:
ΔΘ = 100·ΔΧ/(Χβ-Χο)
Αρα γνωριζοντας τα Χο και Χβ και σημειωνοντας τα πανω στο οργανο(πχ υδραργυρικο θερμομετρο), μπορουμε να χωρισουμε σε 100 ισα διαστηματα το διαστημα μεταξυ τους και ετσι καθε να κατασκευασουμε ενα θερμομετρο οπου η ενδειξη του Χο θα αντιστοιχει σε θερμοκρασια Θο που την λεμε 0 βαθμοι Κελσιου, η ενδειξη του Χβ θα αντιστοιχει σε θερμοκρασια Θτ που την λεμε 100 βαθμοι Κελσιου, η θερμοκρασια στο 3ο πχ σημειο απο το Θο αντιστοιχει σε θερμοκρασια 3 βαθμων Κελσιου κλπ. Επειτα προεκτεινουμε την κλιμακα και εξω απο το διαστημα [0 , +100] με τον ιδιο τροπο αφου ισα διαστηματα σημαινουν και ισες θερμοκρασιες.
Ενω το συμβολο των βαθμων Κελσιου ειναι το °C και αναμεσα σε αυτο και την αριθμητικη τιμη της θερμοκρασιας πρεπει να μπαινει ενα ακριβως κενο, οποτε πρεπει να γραφουμε πχ +8 °C ή 43 °C ή -5 °C και οχι 4°C ή 12° C ή 5 C ή 11 °c κλπ.

Μετα το 1954 ομως, για τον ορισμο της κλιμακας Κελσιου, αποφασιστηκε η επιλογη ενος μόνο σημειου και οχι 2 οπως πιο πριν.
Αυτο εγινε ως εξης:
Παιρνοντας την (2) εχουμε οτι Χ/Χο = 1+ α(Θ-Θο)

Εστω τωρα οτι σε θερμοκρασια Θ1 η τιμη της θερμομετρικης ιδιοτητας γινεται 0 και η Θο = 0 οπως και πριν, αρα θα ισχυει 0 = 1 + α·Θ1
Αρα και Θ1 = -1/α
Οποτε η Θ1 ειναι η ελαχιστη θερμοκρασια που μπορει να επιτευχθει μιας και η θερμομετρικη ιδιοτητα δεν γινεται να γινει αρνητικη. Ειναι η θερμοκρασια του απολυτου μηδεν δηλαδη.

Θελοντας τωρα να φτιαξουμε μια αλλη κλιμακα θερμοκρασιας οπου στην αρχη της κλιμακας θερμοκρασιας μας η θερμομετρικη ιδιοτητα να λαμβανει την τιμη 0 και ονομαζοντας Το την θερμοκρασια αυτη και Τ την νεα αυτη κλιμακα θερμοκρασιας θα εχουμε:
Το = -Θ1 = 1/α (3)

οποτε απο την (2) ισχυει οτι:
Χ/Χο = 1 + α(Τ-Το) αρα λογω (3):
Χ/Χο = 1 + α(Τ – 1/α) αρα:
Χ/Χο = α·Τ αρα:
Χ/Χο = Τ/Το αρα τελικα:
Τ = Το·Χ/Χο

Οποτε επιτυχαμε τον σκοπο μας αφου με μια μετρηση της καταστασης Χο,Το φτιαχνουμε την κλιμακα θερμοκρασιας μας.
Αρκει να μετρησουμε τον λογο των ποσοτητων Χο,Χ.
Χρησιμοποιωντας διάφορα αερια και την πιεση P ως θερμομετρικη ιδιοτητα(X=P) βρηκαμε οτι για ολα τα αερια σε πολυ πολυ χαμηλη πιεση(Po) ισχυει:
Τβ/Το = 1.3661 (4)
και Τ = Το·P/Po

Η μοναδα θερμοκρασιας τωρα που αντιστοιχει στα παραπανω οριστηκε να ειναι το Kelvin (συμβολο Κ) με την αυθαιρετη επιλογη οτι μεταξυ των θερμοκρασιων Το και Τβ να υπαρχει θερμοκρασιακη διαφορά 100 Κελβιν.
Δηλαδη Τβ-Το = 100 αρα και με βαση την (4) ισχυει:
100 + Το = 1.3661·Το οποτε και Το ≈ 273.15 Κ

Και λογω του ορισμου των βαθμων Κελσιου που δινουν την ιδια διαφορά μεταξυ των καταστασεων Θο,Θβ θα ισχυει οτι οι 2 κλιμακες συνδεονται με την σχεση:
Τ/Κ = Θ/°C + 273.15
Οπου Τ η θερμοκρασια σε βαθμους Κελβιν και Θ η θερμοκρασια σε βαθμους Κελσιου

Ετσι το απολυτο μηδεν θερμοκρασιας, η ελαχιστη θερμοκρασια δηλαδη που μπορει αν υπαρξει στον κοσμο ειναι οι 0 βαθμοι Κελβιν (0 Κ) ή ισοδυναμα οι -273.15 βαθμοι Κελσιου (-273.15 °C).
Ισχυει δηλαδη 0 Κ = -273.15 °C

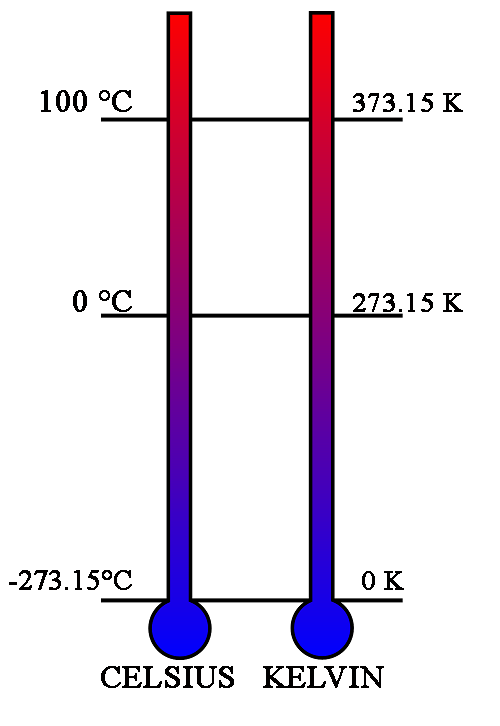
Η κλιμακα Κελβιν ειναι μια κλιμακα θερμοκρασιας που μετραει την απολυτη θερμοκρασια, δειχνει δηλαδη αμεσα(ειναι ευθεως αναλογη) την ποσοτητα της κινητικης ενεργειας των μοριων του σωματος ως προς τις εσωτερικες κινησεις τους, σε αντιθεση με την κλιμακα Κελσιου που ειναι εμπειρικη κλιμακα θερμοκρασιας και δεν αντιστοιχει αμεσα σε καποια τιμη της εσωτερικης ενεργειας.

Για να επανελθουμε στην κλιμακα Κελσιου, μετα το 1954 λοιπον, αποφασιστηκε να μην λαμβανονται τα σημεια παγου (0 °C) και σημεια βρασμου (+100 °C) ως τα 2 σημεια που σχεδιαζεται η κλιμακα Κελσιου αλλά μόνο 1 σημειο, αυτο του τριπλου σημειου του νερου, της καταστασης δηλαδη στην οποια υγρο νερο, νερο σε μορφη παγου αλλά και αεριου συνυπαρχουν και βρισκονται σε ισορροπια κατω απο συνθηκες πιεσης 611.657 Pa.
Η θερμοκρασια του τριπλου νερου κατω απο αυτη την πιεση ειναι 0.0075 °C ή σε προσεγγιση 0.01 °C.
Υπο αυτη την νεα θεωρηση λοιπον, η νεα Το γινεται Το = 273.16 Κ ενω η σχεση κλιμακας Κελσιου και Κελβιν δεν αλλαζει και παραμενει η Τ/Κ = Θ/°C + 273.15
Φυσικα το απολυτο μηδεν παραμεινει το -273.15 °C = 0 K

Στην επιστημονικη βιβλιογραφια, η χρηση της θερμοκρασιας Κελβιν ειναι μονοδρομος στις περισσοτερες περιπτωσεις αναλυσης φυσικων διεργασιων, με παραλληλη χρηση και της κλιμακας Κελσιου για περιπτωσεις στατιστικης καταγραφης κυριως.
Βεβαια μια αλλη, σχετικα διαδεδομενη σε ορισμενες συγκεκριμενες χωρες, κλιμακα εμπειρικης θερμοκρασιας ειναι η κλιμακα Φαρενάιτ οπου χρησιμοποιειται αποκλειστικα εναντι της κλιμακας Κελσιου, στις ΗΠΑ, στις Μπαχαμες, στα νησια Κέιμαν, Λιβερια και σε μερικές αλλες χωρες, ενω στον Καναδα, στο Ηνωμενο Βασιλειο και σε μερικες αλλες χωρες χρησιμοποιουνται και οι 3 κλιμακες.
Η κλιμακα Φαρενάιτ(F) σε σχεση με την κλιμακα Κελσιου(Θ) ειναι:
Οπου F η θερμοκρασια σε βαθμους Φαρενάιτ και Θ η θερμοκρασια σε βαθμους Κελσιου
Δηλαδη για 14 °F εχουμε Θ = (5/9)·(14 – 32) °C = -10 °C
Ενω για -40 βαθμους Φαρενάιτ η αντιστοιχη θερμοκρασια σε βαθμους Κελσιου ειναι επισης -40 °C.

Please follow and like us: